This post is a full breakdown of how to analyze and graph sine functions, including how to extract amplitude, period, and phase shift from a transformed equation. The focus is on the function:

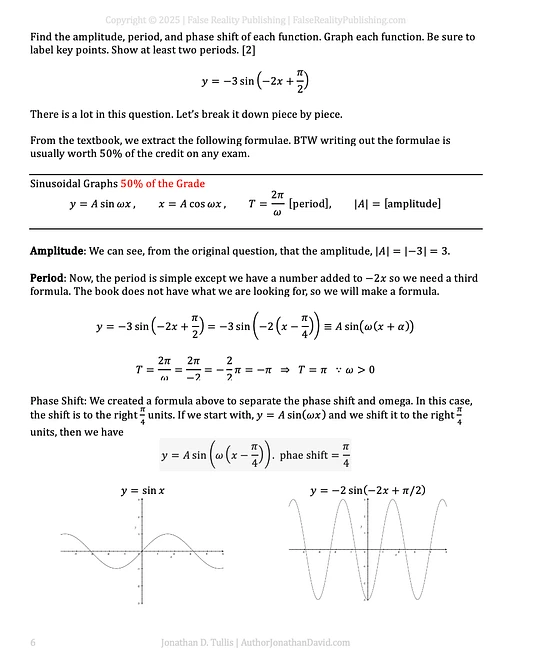
y = –3·sin(–2x + π/2)

Using the standard sinusoidal form y = A·sin(ωx + φ), the image guides you through:

• Amplitude: |A| = 3

• Period: T = 2π / |–2| = π

• Phase Shift: π/4 units to the right, found by rewriting the expression into the form –2(x – π/4)

It explains how to:

• Use the standard formula for period and phase shift

• Recognize that a negative ω value does not change the period since it's based on |ω|

• Identify how amplitude reflects the height of the wave from midline to crest

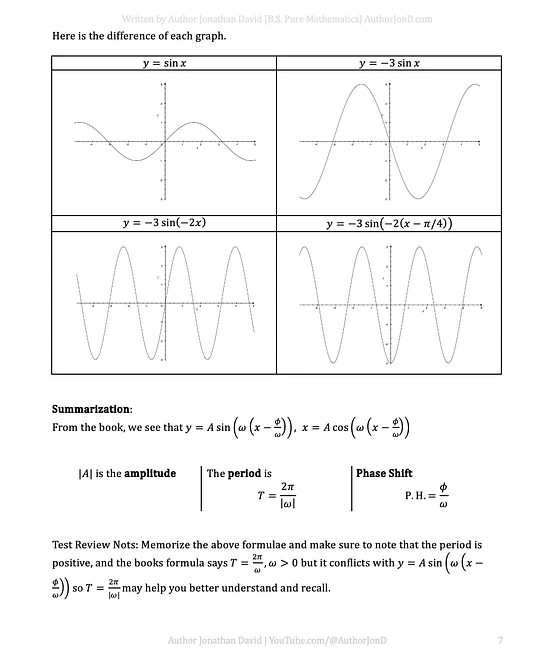
The second page includes side-by-side graphs comparing:

• y = sin(x)

• y = –3·sin(x)

• y = –3·sin(–2x)

• y = –3·sin(–2(x – π/4))

These visual comparisons help you see how each transformation affects the graph—whether it’s a reflection, vertical stretch, horizontal compression, or a phase shift.

These visuals are taken directly from the Ultimate Crash Course for STEM Majors, which includes graphing techniques, trigonometric transformations, and test-prep strategies for every major topic in college algebra and precalculus.

Get the complete guide with lifetime access:
https://author-jonathan-david-shop.fourthwall.com/products/the-ultimate-crash-course-includes-bonus-ultimate-cheat-sheet-800-pages-of-goodness

View all resources and bundles here:
https://author-jonathan-david-shop.fourthwall.com

Search tags: find amplitude and phase shift, how to graph sine functions, period of sine curve, y = –3·sin(–2x + π/2), trig transformations graph, phase shift explained, sinusoidal formula graph, graphing trigonometry step-by-step.