Title: How to Find a Line Parallel to a Given One – Step-by-Step Formula and Graph Guide

This post explains how to find the equation of a line that passes through a given point and is parallel to a given line. It’s a must-know skill in algebra and coordinate geometry, and a common question on exams.

The Problem:
Find the line that passes through the point (1,1) and is parallel to the line 2x – 5y = 10.

Step-by-Step Breakdown:

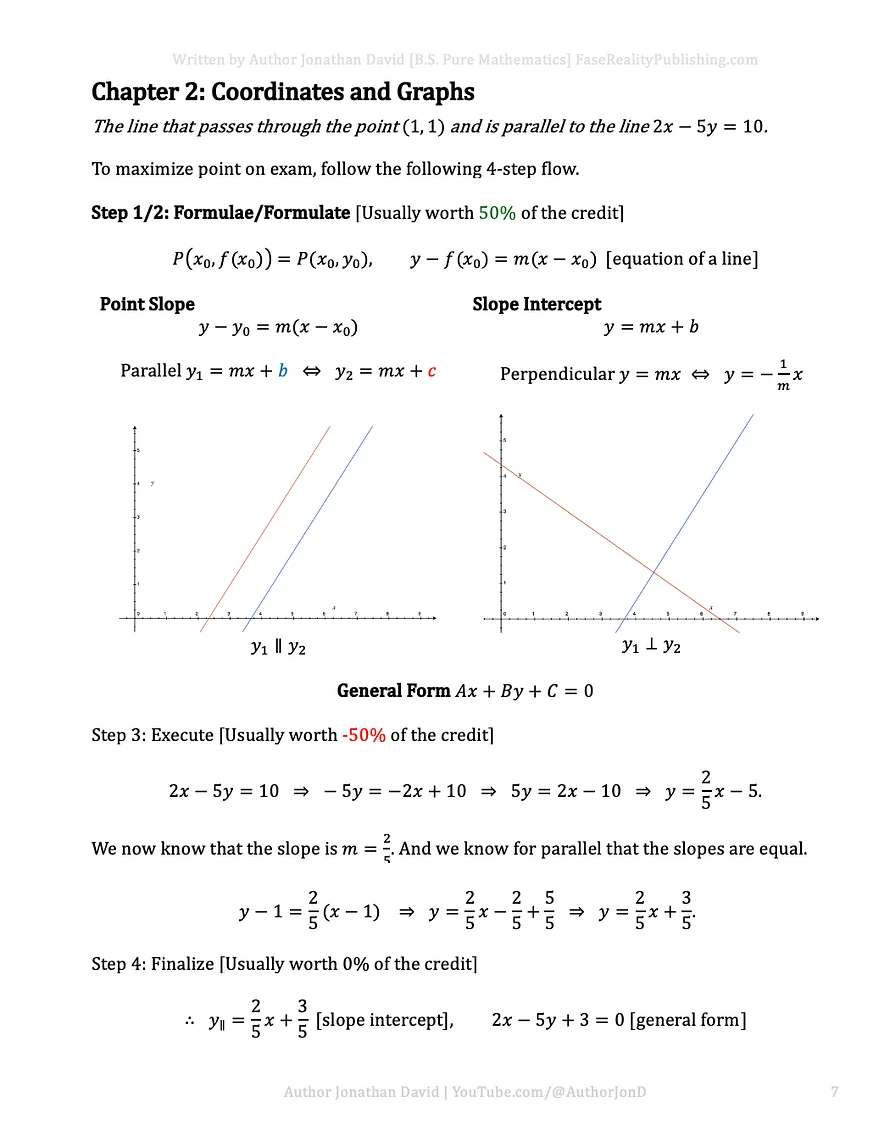
Step 1/2: Formulae/Formulate
Start with the point-slope form:
y – y₁ = m(x – x₁)
And remember: parallel lines have the same slope.

Step 3: Execute
Rearrange the given line into slope-intercept form:
2x – 5y = 10 → y = (2/5)x – 2
The slope is m = 2/5. Use the point (1, 1) to plug into the formula:
y – 1 = (2/5)(x – 1) → y = (2/5)x + 3/5

Step 4: Finalize
Write both forms:
Slope-intercept: y = (2/5)x + 3/5
General form: 2x – 5y + 3 = 0

The guide includes color-coded graphs that show how to identify parallel and perpendicular lines visually, and reminds you how credit is distributed on exams: setting up the formula is 50%, doing the work is another 50%, and final boxing gets 0% unless everything else is right.

This is taken from Chapter 2 of the Ultimate Crash Course for STEM Majors, designed to help students succeed in coordinate geometry, precalculus, and physics.

Get lifetime access to the full 800+ page PDF here:
https://author-jonathan-david-shop.fourthwall.com/products/the-ultimate-crash-course-includes-bonus-ultimate-cheat-sheet-800-pages-of-goodness

Browse the full shop for bundles and guides:
https://author-jonathan-david-shop.fourthwall.com

Search tags: find parallel line equation, point slope form example, algebra line through point, slope intercept form, convert to general form, line parallel to 2x – 5y = 10, how to use point-slope formula, graphing parallel and perpendicular lines.